
Biography
Hong-Ming Chiu is a Electrical and Computer Engineering PhD student at the University of Illinois Urbana-Champaign (UIUC), working with Prof. Richard Y. Zhang. He received his Bachelor's Degree in Electronics Engineering from National Yang Ming Chiao Tung University, Hsinchu, Taiwan (NYCU). He worked with Prof. Carrson C. Fung and Prof. Tian-Sheuan Chang during his undergrads. He is a member of IEEE-Eta Kappa Nu, Mu Sigma Chapter and a former member of IEEE Student Bench at NYCU. His research interests include Machine Learning and Optimization.
Experiences
 Ph.D. student @ UIUC
Ph.D. student @ UIUC Research Assistant @ NYCU
Research Assistant @ NYCU
 Exchange Student @ UIUC
Exchange Student @ UIUC
 Summer Research @ USC
Summer Research @ USC Undergraduate Researcher @
NYCU
Undergraduate Researcher @
NYCU Undergraduate Researcher @
NYCU
Undergraduate Researcher @
NYCUPublications

We exploit the low-rank structure in an SDP to reduce the per-iteration cost of IPM down to cubic time and quadratic memory. A traditional difficulty is the dense Newton subproblem at each iteration, which becomes progressively ill-conditioned as progress is made towards the solution. We present a well-conditioned reformulation of the Newton subproblem whose condition number is guaranteed to remain bounded over all iterations, as well as a well-conditioned preconditioner that greatly improves the convergence of the inner iterations.
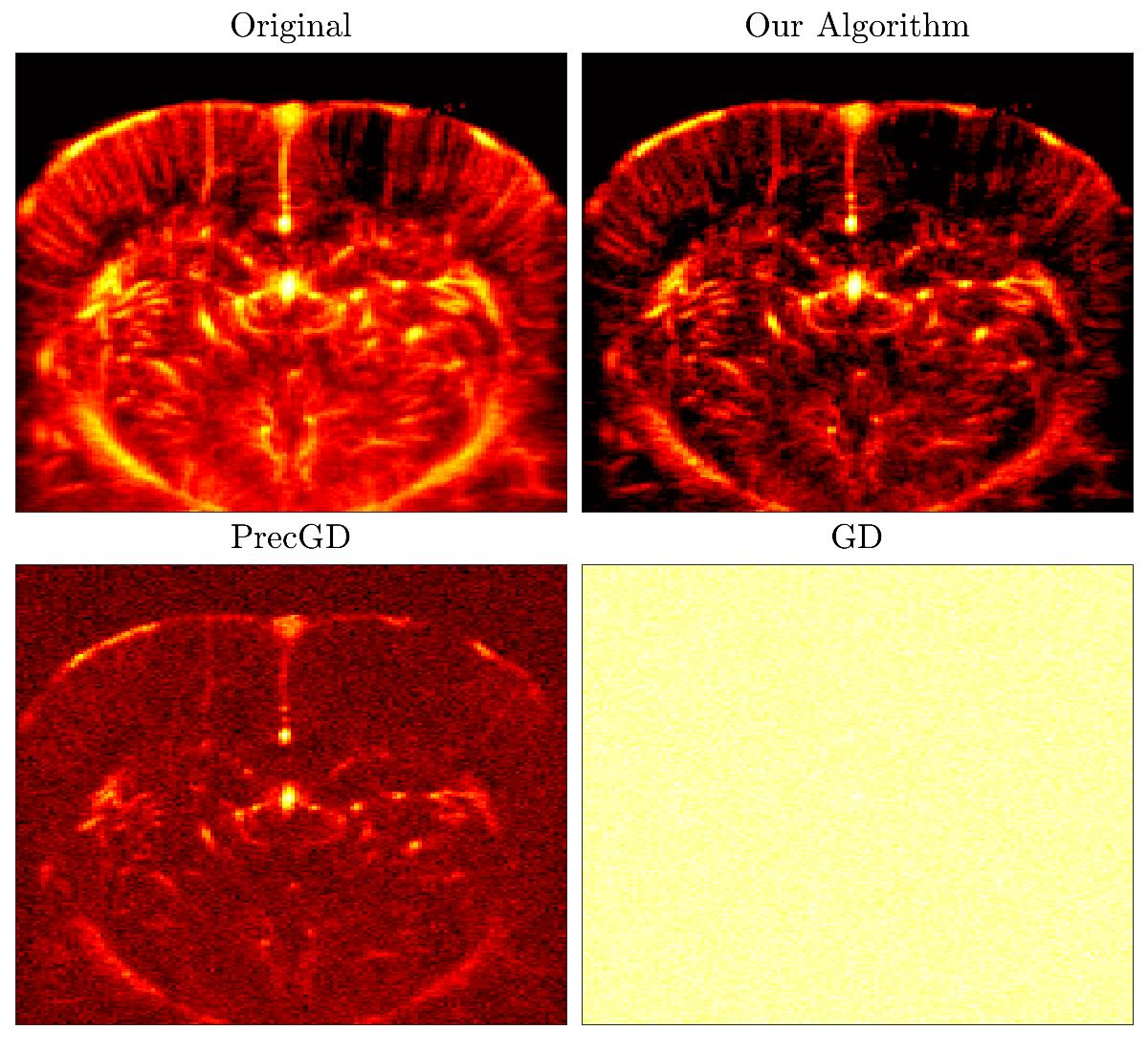
When comparing different methods for statistical estimation, one of the most important criteria is whether the given estimator can achieve a minimax error: an estimator achieves the best possible risk in the worst possible scenario if it is minimax optimal. Our interest in minimax error estimations arise from medical imaging applications, where the highest possible level of reconstruction accuracy is desired, in order to minimize the chances of diagnostic errors, detect subtle changes or anomalies, and reduce the need for repeated scans or reanalysis.

To certify robustness of neural networks, most techniques rely on solving linear programming (LP) relaxations. However, recent results suggest that all LP relaxations face an inherent "convex relaxation barrier" that prevent them from making high-quality certifications. In this paper, we propose a new certification technique based on nonconvex rank-restricted semidefinite programming (SDP) relaxations that can overcome the "convex relaxation barrier" faced by the LP relaxation.
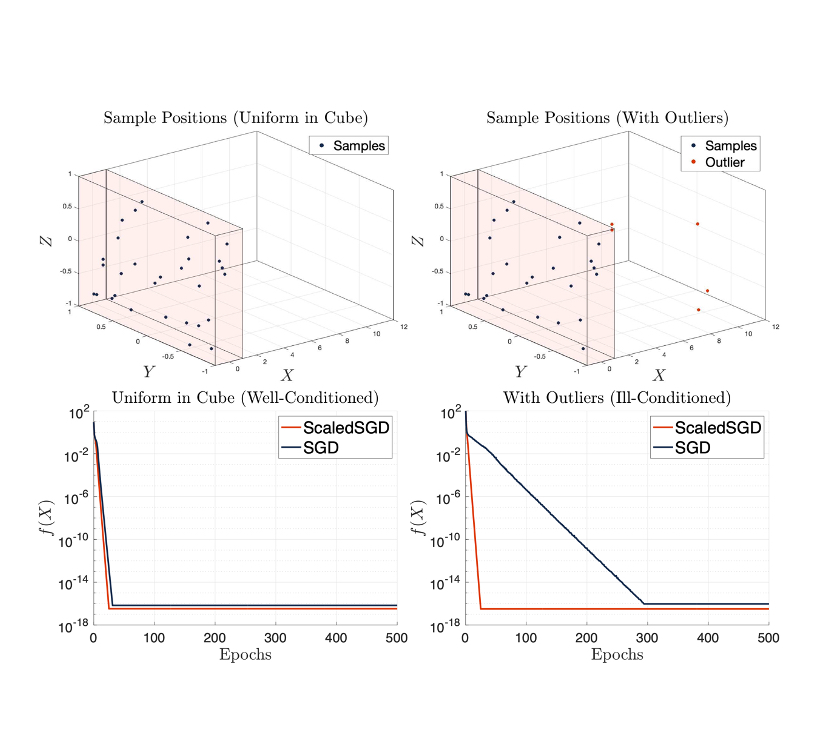
The matrix completion problem seeks to recover a $d \times d$ ground truth matrix of low rank $r \ll d$ from observations of its individual elements. Stochastic gradient descent (SGD) is one of the few algorithms capable of solving matrix completion on a huge scale. Unfortunately, SGD experiences a dramatic slow-down when the underlying ground truth is ill-conditioned; it requires at least $O(\kappa \log(1/\epsilon))$ iterations to get $\epsilon$-close to ground truth matrix with condition number $\kappa$. In this paper, we propose a preconditioned version of SGD that is agnostic to $\kappa$. For a symmetric ground truth and the Root Mean Square Error (RMSE) loss, we prove that the preconditioned SGD converges in $O(\log(1/\epsilon))$ iterations.
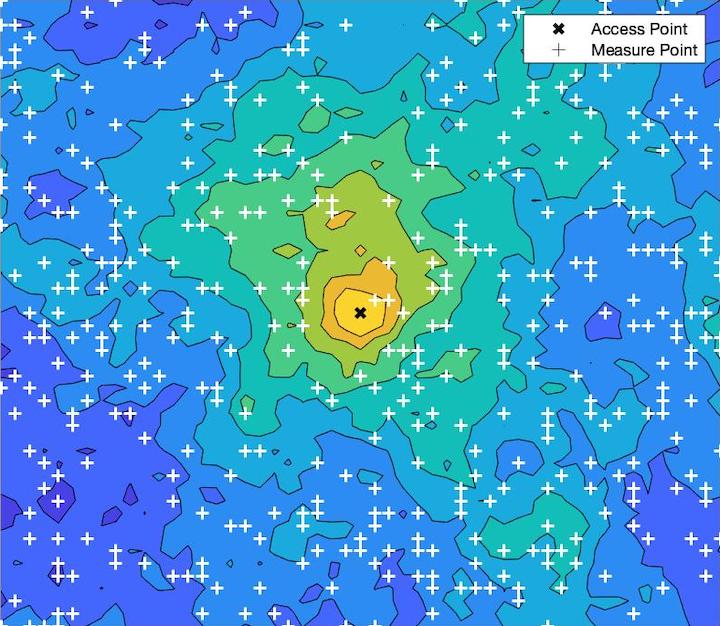
A graph learning and augmentation (GLA) technique is proposed herein to solve the received signal power interpolation problem, which is important for preemptive resource allocation in location-aware communications. A graph parameterization results in the proposed GLA interpolator having superior mean-squared error performance and lower computational complexity than the traditional Gaussian process method. Simulation results and analytical complexity analysis are used to prove the efficacy of the GLA interpolator.
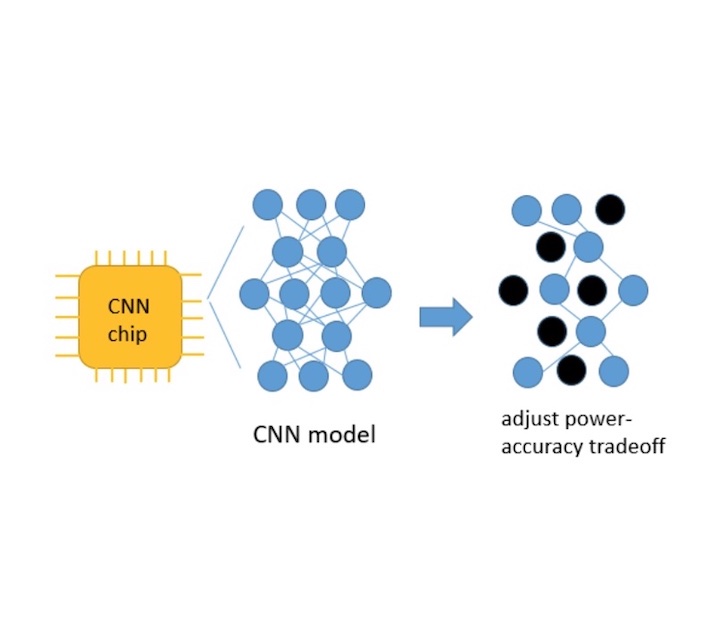
Modern convolutional neural network (CNN) models offer significant performance improvement over previous methods, but suffer from high computational complexity and are not able to adapt to different run-time needs. To solve the above problem, this paper proposes an inference-stage pruning method that offers multiple operation points in a single model, which can provide computational power-accuracy modulation during run time. This method can perform on shallow CNN models as well as very deep networks such as Resnet101. Experimental results show that up to 50% savings in the FLOP are available by trading away less than 10% of the top-1 accuracy.
Projects
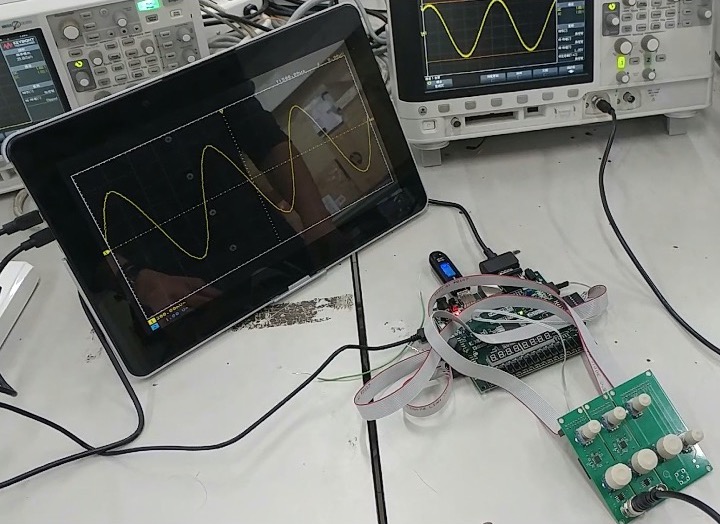
We built a simple oscilloscope using Nexys 4 DDR board and PCB. First, the PCB transforms the input voltage signal into a signal with an acceptable voltage range for the FPGA board input, as well as generating knobs' control signal. The FPGA board then takes the processed signal and control signal to display waveforms, change voltage scale, adjust sweep time, etc. This work is the final project of the Digital Laboratory class at NYCU.
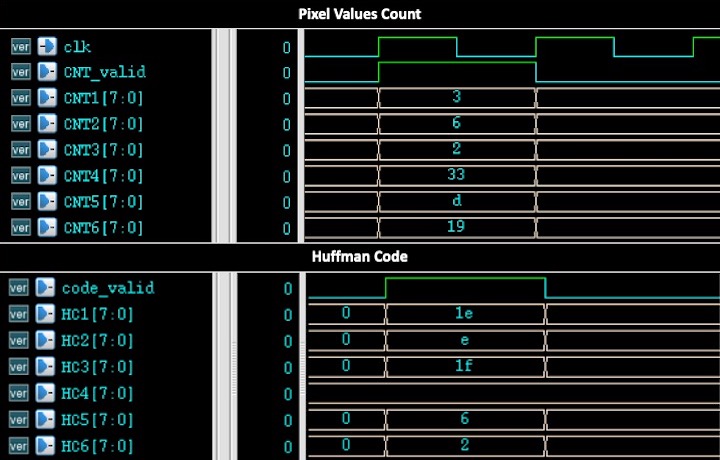
Implemented 8-bit Huffman coding algorithm using System Verilog. The system takes an image as an input, the image contains 100 pixels and each pixel value is an integer between 1 to 6 (inclusive). The system then outputs the Huffman Code for each pixel value based on the source probability distribution (more frequent pixel values will have the shorter codewords). This is the final project of the Digital Circuit and Systems class in NYCU.